Problems 60+

Problem No. 61

Problem No. 61

by 123iitjee.com Support -
Number of replies: 0
Consider a satellite. Under the action of central force obeying the inverse-square law, bodies follow trajectories described by ellipses, parabolas or hyperbolas. In the approximation m <<M the gravitating mass M is at one of the focuses. 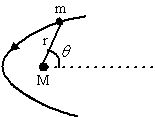fig.

Taking the origin at this focus, the general polar equation of these curves can be written as, \(r(\theta)=\frac{l}{1-e\cos\theta}\).

Where l is the semi-latus-rectum and e is the eccentricity of the curve. In terms of the constants of the motion:

\(l=\frac{L^2}{GMm^2}\) and e=\(\left({1+{{2EL^2}\over {G^2 M^2 m^3 }}}\right)^{1/2}\).

Where G is the Universal Gravitational constant, L is the modulus of the angular momentum of the orbiting mass with respect to the origin and E is the mechanical energy, with zero potential energy at infinity.

We may have the following cases:
  1. If \(0\le e<1\), the curve is an ellipse (circle for e=0).
  2. If e=1, the curve is a parabola.
  3. If e > 1, the curve is a hyperbola.
Now, consider an Earth's geosynchronous satellite orbiting in circular path (the radius r0 and speed v0 can be found by you). A small rocket is fired from it which imparts a thrust directed towards Earth causing velocity variation \(\Delta v\). This variation can be assumed to have occurred instantaneously. 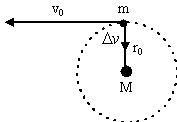fig.

Answer the following questions based on this:
  1. What is the expression for r0 - the equatorial radius of the geosynchronous satellite - as a function of g, R and any other known constant. Where R is the radius of the Earth.
  2. What is the expression for the earlier velocity v0 as a function of g, R and r0?
  3. What is the expression for earlier angular momentum L0 as a function of v0, m, g and R?
  4. What is the expression for earlier mechanical energy E0 as a function of v0, m?
  5. What is the expression for l in terms of r0 after rocket is fired?
  6. What is the expression for e in terms of v0 and \(\Delta v\) after rocket is fired? Hence predict the shape of trajectory of satellite.

Submission Closed

Cracked By:

1. Rajat Goel, 12th, Lucknow Public College, Lucknow.
2. Varun Agrawal, 12th, DPS, Vindhyanagar, Sidhi.
3. Amarpreet Singh Bir, 12th Pass (Govt. Mohindra College), Patiala.
4. Mohd Saad Bhamla, 1st Year, Computer Science, VESIT (Vivekanand College), Mumbai.

Varun's solution (.pdf) is attached.