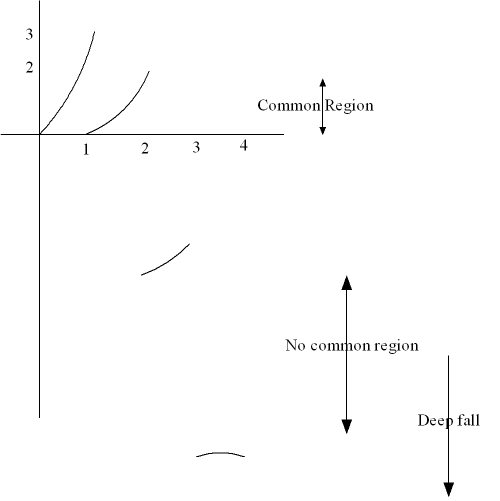
On first thought, consider, x2 -3x[x] + 2x for positive values of x:
\(0\le x<1\), x2-3x[x]+2x=x2+2x lies between 0 to 3
\(1\le x<2\), x2-3x[x]+2x=x2-x lies between 0 to 2
\(2\le x<3\), x2-3x[x]+2x=x2-4x lies between -4 to -3
\(3\le x<4\), x2-3x[x]+2x=x2-7x which is around -12
\(4\le x<5\), x2-3x[x]+2x=x2-10x lies between -24 to -25
& so on ..................................
The rough graph is attached. As can be seen from the figure, if the graph is shifted downwards by any value between 0+h to 2-h (h is a small positive number ---> 0), then the graph would cut x-axis at two points (see the common region). a should lie between the same two values, i.e. 0 to 2 as we are interested in x2-3x[x]+2x-a and subtracting a from x2-3x[x]+2x shifts the graph downwards.
thanks sir